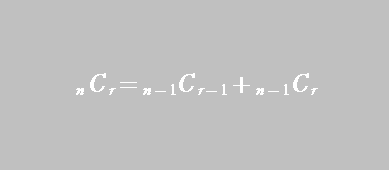
今回は次の等式について考えます。
はじめに
ただでさえ難しい式で,
解説を見ても
「特定の一つのものに注目する。」
「含む場合と含まない場合に分けて考える。」
の表現にピンと来ないのではないでしょうか。
分かりやすくするために,数字を使って考えてみましょう。
等式の考え方
4人の中から3人を選ぶとき,選び方の総数は 4C3 = 4 (通り)です。
A , B , C , D の4人で考えると,組の数は
![]()
の4通り。
ここで,A を含むかどうかで分けると

と分けられます。
A を含む3組について
A を含む3組は BC , BD , CD に A をくっつけた組と考えられるので
B , C , D の3人から2人を選ぶ 3C2 = 3 (通り) と同じになりますね。

A を含まない1組について
A を含まない1組は,( A 以外の) B , C , D の3人から3人を選ぶ 3C3 = 1 (通り)

まとめ
4人の中にA を含むかどうかで考えれば
![]()
の式が成り立ちますね。
これを n , r に戻して考えれば
” n 人の中から r 人を選び出すとき, n 人の中の特定の1人 A に着目すると
r 人の中に A を含む組の数は n-1Cr-1
A を含まない組の数は n-1Cr
従って,nCr = n-1Cr-1 + n-1Cr が成り立つ。”
おわりに
いかがでしょうか。
難しそうに見える式は,数字を当てはめることで手がかりが見えてきそうですね。