気ままな数学ノート

「調べても分からない」に寄り添う

【数列】群数列を階差数列で解いてはいけない？

数学

今回は記述式回答で注意してほしい群数列の解き方を紹介します。

◎問題

　４で割ると１あまる数列を

１｜５，９｜１３，１７，２１｜２５，・・・

のように第ｎ群がｎ個の数を含むように分けるとき

第ｎ群の最初の数を求めよ。

群数列の解き方

　4 で割ると 1 余る数は $4m-3(m:整数)$ と表せる。

$n\geqq2$ のとき

　第１群から第 $(n-1)$ 群までにある数の個数は

　 $1+2+3+・・・+(n-1)=\frac{1}{2}(n-1)n$

よって，第 n 群の最初の数は $\frac{1}{2}(n-1)n+1$ 番目の数で

$4・\frac{1}{2}(n-1)n+1-3=2n^2-2n-3$

　これは $n=1$ のときも成り立つ。

群数列を階差数列を用いて解く

　各群の最初の数 $1,5,13,25,・・・$ この数列を $a_n$ とする。

　数列 { $a_n$ } の階差数列を { $b_n$ } とすると

　{ $b_n$ }： $4,8,12,・・・$

　よって一般項は $b_n=4n$

　これより，数列 { $a_n$ } の一般項は

　 $n\geqq2$ のとき

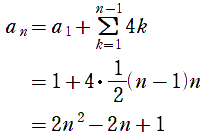
　 f:id:Peroki:20210320221121p:plain

　これは $n=1$ のときも成り立つ。

しかし，この解き方は完璧であるとは言えない。

階差数列を用いてはいけない理由

　ここで問題となるのは，各群の最初の数列 { $a_n$ }

　{ $a_n$ }： $1,5,13,25,・・・$ に対して考えた階差数列

　{ $b_n$ }： $4,8,12,・・・$ が 4 の倍数であると推測して話を進めている点である。

　感覚的には 4 の倍数と思えるが，この問題において数列 { $b_n$ } がどこまでも規則的に増える保証はない。

　記述で無ければアリかもしれないが，記述式回答であるならば数学的帰納法を用いて数列 { $b_n$ } の一般項が $b_n=4n$ となることを示す必要がある。

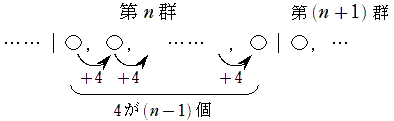
　せめて，「第 n 群に n 個の数が含まれるとき，第 n 群の最後の数は第 n 群の最初の数に 4(n-1) を足したものとなる。第 n 群の最後の数に 4 を足したものが第 (n+1) 群の最初の数なので，第 (n+1) 群の最初の数は第 n 群の最初の数に $4(n-1)+4=4n$ を足したものといえる。」などと書いておくことを勧める。

f:id:Peroki:20210320221117p:plain — イメージ

備考

　受験では群数列を階差数列で解いてはいけない。とよく耳にするが，考えれば考えるほどなぜいけないのかの理由が曖昧になってしまうのも事実である。

　教科書などの階差数列の問題も，元の数列の階差数列が規則を持っている前提で話を進めていることが多い。（証明もなしに）
　（※ここ数年では，「階差数列を利用して」の一文を載せることが増えてきた。）

　これに対して何か知っていらっしゃる方がいればコメントを頂きたい。