気ままな数学ノート

「調べても分からない」に寄り添う

【対数】10の△乗の桁数、小数第〇位の考え方を分かりやすく解説します

数学

ｎは〇桁の数である
- 簡単な数で確かめる
- ｎについて考える
ｎは小数第◯位で初めて0以外の数が現れる
- 簡単な数で考える
- ｎで考える
まとめ

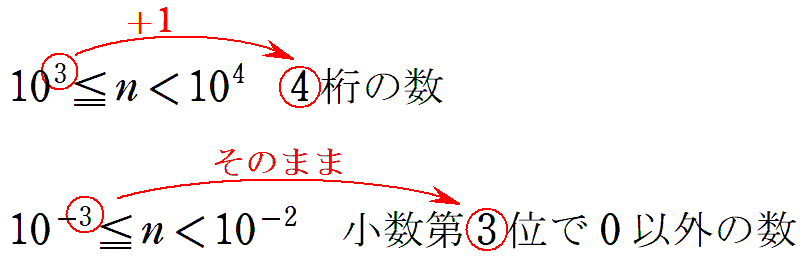
どの数字に注目すればいいのか混乱しがちなこの問題
$n$ は◯桁の数、小数第◯位の考え方について解説します

ｎは〇桁の数である
- 簡単な数で確かめる
- ｎについて考える
ｎは小数第◯位で初めて0以外の数が現れる
- 簡単な数で考える
- ｎで考える
まとめ

ｎは〇桁の数である

簡単な数で確かめる

例えば，519 は
　 $100\leq{519}\lt{1000}$
　つまり
　 $10^2\leq{519}\lt{10^3}$ と表せる

ここで，
　
　 $10^2$ は 1 の後ろに 0 が 2 個ある数なので
　 $10^2$ は 3 桁の数である

$3 桁\leq{519}\lt 4 桁$ と見れば、519 は 3 桁の数と言えますね

ｎについて考える

数が大きくなっても同じように考えると

　 $10^8\leq{n}\lt10^9$ のとき
　 $10^8$ は 1 の後ろに 0 が 8 個あるので 9 桁の数
　 $10^9$ は 1 の後ろに 0 が 9 個あるので 10 桁の数

「 $9 桁\leq{n}\lt10 桁$ 」と見れば、 $n$ が 9 桁の数だと分かります

ｎは小数第◯位で初めて0以外の数が現れる

簡単な数で考える

例えば，0.09 は
　 $0.01\leq0.09\lt0.1$
　つまり
　 $10^{-2}\leq0.09\lt10^{-1}$ と表せる

ここで，
　
　 $10^{-2}$ は 1 の前に 0 が 2 つ続く小数なので
　 $10^{-2}$ は小数第 2 位で初めて 1 が現れる数と言える

「 $小数第２位が１の数\leq0.09\lt小数第１位が１の数$ 」と見れば、 $n$ は小数第 2 位で初めて 0 以外の数が現れると分かりますね

ｎで考える

数が小さくなっても同じように考えると

　 $10^{-5}\leq{n}\lt10^{-4}$ のとき
　 $10^{-5}$ は 1 の前に 0 が 5 つ続く小数なので
　 $10^{-5}$ は小数第 5 位で初めて 1 が現れる数と言える

「 $小数第５位が１の数\leq{n}\lt小数第４位が１の数$ 」と考えれば， $n$ は小数第 5 位で初めて 0以外の数が現れると言えますね

まとめ

桁や位を求めるときに，どの指数に注目すればいいのか分からなくなってしまったときは具体的な数字を使って考えるといいですね