気ままな数学ノート

「調べても分からない」に寄り添う

【図形・ベクトル】外分点はとりあえず書いてみると分かりやすい

数学

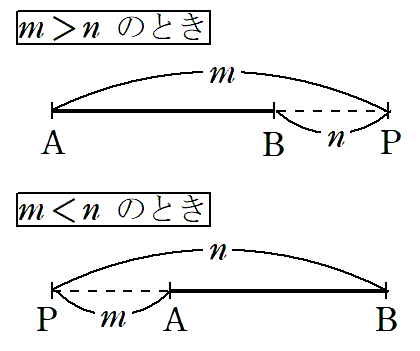
線分ABを外分するとき，左側と右側のどちらに点を取ればいいのか分からなくなったときの方法を紹介します

1）ＡＢを 1 : 2 に内分する点Ｐ
2）ＡＢを 2 : 5 に外分する点Ｑ
- 「適当に書いてみる」が大切
3）ＡＢを 5 : 2 に外分する点Ｒ
4）ＢＡを 2 : 5 に外分する点Ｓ
まとめ

◎問題

次の点を図示しなさい

（1）線分ＡＢを 1 : 2 に内分する点Ｐ
（2）線分ＡＢを 2 : 5 に外分する点Ｑ
（3）線分ＡＢを 5 : 2 に外分する点Ｒ
（4）線分ＢＡを 2 : 5 に外分する点Ｓ

1）ＡＢを 1 : 2 に内分する点Ｐ

線分ＡＢを分ける点がＰなので
　 $AP:PB=1:2$
　となる点Ｐをとると

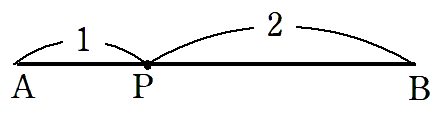
2）ＡＢを 2 : 5 に外分する点Ｑ

線分ＡＢを分ける点がＱなので
　 $AQ:QB=2:5$
　となる外分点を考えます

「適当に書いてみる」が大切

例えば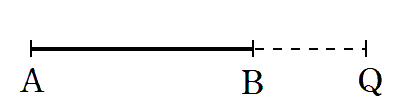

この位置に点Ｑをとると

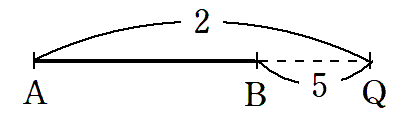
これでは
　 $AQ:QB=2:5$ になりません

ここで，反対側に点Ｑをとると

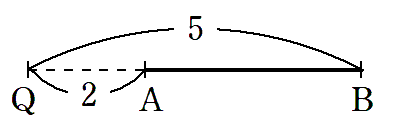
これで
　 $AQ:QB=2:5$ となりました

3）ＡＢを 5 : 2 に外分する点Ｒ

線分ＡＢを分ける点がＲなので
　 $AR:RB=5:2$
　となる外分点Ｒをとると

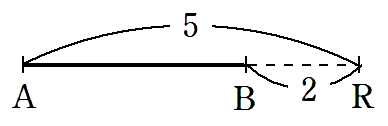
4）ＢＡを 2 : 5 に外分する点Ｓ

線分ＢＡを分ける点がＳなので
　 $BS:SA=2:5$
　となる外分点Ｓをとると

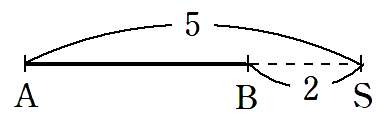
まとめ

線分ＡＢを～分する点■は
　 $A■:■B=〇:〇$
　と考えて

実際に適当な点を取ったときにその比が正しいか
　を考えるとうまく点を取れそうですね