【数学A】nPrとnCrの違いって??

最初はなんとなく理解できていたはずが，
いつの間にか訳が分からなくなってしまう Ｐ と Ｃ 
今回はそんな nPr と nCr の使い分けについて紹介します

この記事の目次

 nPr の考え方

◎問題

A，B，C，D の４人から３人を選んで１列に並べるとき，

何通りの並べ方があるか求めなさい

パターン１．樹形図で考える

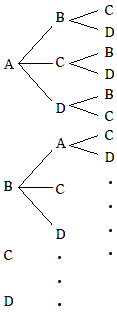
右の樹形図で３人の並び方を考えると

　左　：Ａ，Ｂ，Ｃ，Ｄ の４通り

　中央：左に入らなかった３通り

　右　：残りの２通り

とそれぞれで枝分かれしていくので

（4P3=）４×３×２=２４（通り）

 と考えられます

パターン２．マス目で考える

パターン１と同じ考え方をマス目に置きかえると

　
左から順に ４，３，２(通り）の枝分かれが考えられるので

（4P3=）４×３×２=24（通り）

※ここでの ABC と ACB は違う並び方であることに注意

Point 

nPr を使うのは

 順番をつけて並べるとき

 nCr の考え方

◎問題

A，B，C，D の４人から３人を選ぶとき，

何通りの選び方があるか求めなさい

パターン１．書き出して考える

考えられる組は

 ABC , ABD , ACD , BCDの４通り

パターン２． nPr の考え方を使う

まず，４人から３人を選んで１列に並べると考えると

　並べ方は

　の 24 通り

しかし，同じ人同士を選んでいる重複がそれぞれ６通りずつあるので

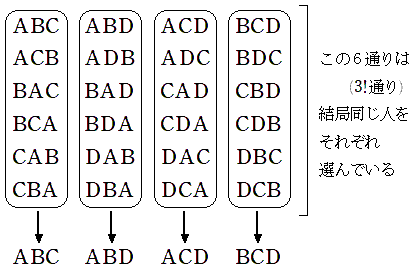
４人から３人を選ぶ組み合わせ 4C3 は

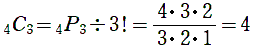
よって，４通りと求められます。

※ここでの ABC と ACB は同じ選び方であることに注意

Point 

nCr を使うのは

順番関係なく選ぶとき

 まとめ

４人のうち３人を

　順序付けて並べるとき… 4P3

　順番関係なく選ぶとき… 4C3

 nPr と nCr の使い分けは”順番を付けるかどうか”と意識しましょう