気ままな数学ノート

「調べても分からない」に寄り添う

【判別式】D/4はxの係数が偶数のときに使う（4分のd）

数学

◎問題

次の２次方程式の解の個数を求めなさい

(1) $x^2-4x+3=0$

(2) $x^2-2(m+1)x+3=0$

解答1)
- 判別式Dを使う
- 判別式D/4を使う
解答2)
- 判別式Dを使う
- 判別式D/4を使う
さいごに

解答1) $x^2-4x+3=0$

判別式Dを使う

$x^2-4x+3=0$ の判別式をDとすると

$D=b^2-4ac$

　 $=(-4)^2-4\cdot1\cdot3$

　 $=4$

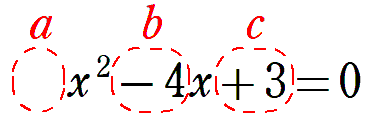
よって， $D\gt0$ から実数解の個数は２つ

判別式D/4を使う

$x^2-4x+3=0$ の判別式をDとすると，D/4は

$D/4={b'}^2-ac$

　　 $=(-2)^2-\cdot1\cdot3$

　　 $=1$

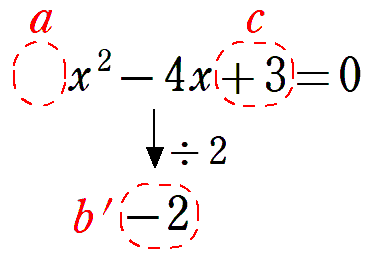
よって， $D\gt0$ から実数解の個数は２つ

解答2) $x^2-2(m+1)x+3=0$

判別式Dを使う

$x^2-2(m+1)x+3=0$ の判別式をDとすると

$D=b^2-4ac$

　　 $={\{-2(m+1)\}}^2-4\cdot1\cdot3$

　　 $=4(m+1)^2-12$

　　 $=4m^2+8m-8$

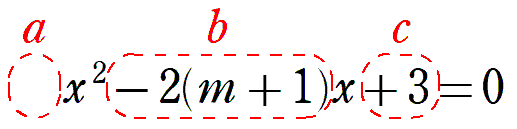
よって，実数解の個数は

　 $m\lt-1-\sqrt{3}$ ， $-1+\sqrt{3}\lt{m}$ のとき２個

　 $m=-1\pm\sqrt{3}$ のとき１個

　 $-1-\sqrt{3}\lt{m}\lt-1+\sqrt{3}$ のとき０個

判別式D/4を使う

$x^2-2(m+1)x+3=0$ の判別式をDとすると

$D/4={b'}^2-ac$

　 $={\{-(m+1)\}}^2-\cdot1\cdot3$

　 $=(m+1)^2-3$

　 $=m^2+2m-2$

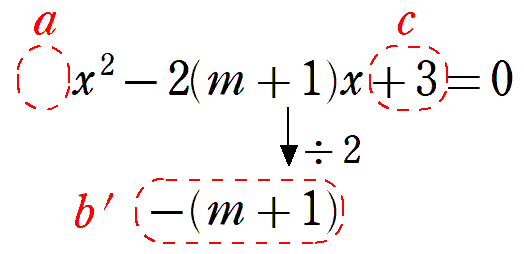
よって，実数解の個数は

　 $m\lt-1-\sqrt{3}$ ， $-1+\sqrt{3}\lt{m}$ のとき２個

　 $m=-1\pm\sqrt{3}$ のとき１個

　 $-1-\sqrt{3}\lt{m}\lt-1+\sqrt{3}$ のとき０個

さいごに

判別式D/4を使えるようになると計算ミスが減り，解く速さも上がるのでマスターしてみてはいかがでしょうか