気ままな数学ノート

「調べても分からない」に寄り添う

2021-03-09 2024-08-22

なぜ？隣接３項間の漸化式

数学

このサイトはアフィリエイト広告（Amazonアソシエイト含む）により収益を得ています

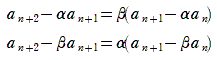
f:id:Peroki:20210309202306p:plain — 隣接３項間の漸化式

　隣接3項間の漸化式でなぜこのような変形ができるのかを考えてみましょう。

もとになる解と係数の関係
解と係数の関係を用いて変形
- ・2次方程式を変形
- ・漸化式で考える
一般項を求める（補足）

もとになる解と係数の関係

◎解と係数の関係

2次方程式 $ax^2+bx+c=0$ の2つの解を $α,β$ とすると

$\displaystyle α+β=-\frac{b}{a}$ ， $\displaystyle αβ=\frac{c}{a}$

とくに $a=1$ のとき

$x^2+bx+c=0$ の2つの解を $α,β$ とすると

$\displaystyle α+β=-b$ ， $\displaystyle αβ=c$

解と係数の関係を用いて変形

・2次方程式を変形

　漸化式 $a_{n+2}+pa_{n+1}+qa_n=0$ を2次方程式 $x^2+px+q=0$ として見る。

この2次方程式の2解が $α,β$ のとき，解と係数の関係から

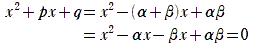
f:id:Peroki:20210309210024p:plain

従って　 $x^2-αx-βx+αβ=0$

　この等式を変形し

$x^2-βx=αx-αβ$ 　から　 $x^2-βx=α(x-β)$

$x^2-αx=βx-αβ$ 　から　 $x^2-αx=β(x-α)$

を得る。

・漸化式で考える

　2次方程式 $x^2+px+q=0$ の異なる2解 $α,β$ を用いて

漸化式 $a_{n+2}+pa_{n+1}+qa_n=0$ を

$a_{n+2}-(α＋β)a_{n+1}+αβa_n=0$ とすれば

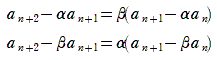
f:id:Peroki:20210309202306p:plain

と変形できる。

一般項を求める（補足）

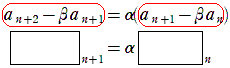
f:id:Peroki:20210309212521p:plain — 等比数列の漸化式の形に

　漸化式 $c_{n+1}=5c_n$ は

数列 { $c_n$ } は初項 $c_1$ 公比 5 の等比数列でした。

　同じように考えると

$a_{n+2}-βa_{n+1}=α(a_{n+1}-βa_n)$

数列 { $a_{n+1}-βa_n$ } は

初項 $a_2-βa_1$ 公比 $α$ の等比数列

$a_{n+2}-αa_{n+1}=β(a_{n+1}-αa_n)$

数列 { $a_{n+1}-αa_n$ } は

初項 $a_2-αa_1$ 公比 $β$ の等比数列

２つの式

　 $a_{n+1}-βa_n=…$

　 $a_{n+1}-αa_n=…$

を連立させれば一般項 $a_n$ を求めることができますね。

ランキング参加中

数学・科学・工学

ランキング参加中